Have a Look at the Bayes Rule Equation Again

Bayes' Theorem Probability

An introduction to a fundamental lesson in Information Science.

One of the nearly important concepts nosotros tin know in Data Science is Bayes' Theorem. Named after the British mathematician and Presbyterian minister Thomas Bayes (18th century), Bayes' theory is congenital on conditional probability. Bayes allows united states of america to deductively reason our mode into estimating unknown probabilities. His logic was true in that because we simply don't know our reality perfectly, we can only improve our knowledge and assumptions when presented with new evidence.

Photo by Tim Mossholder on Unsplash

Applications of the Bayes' Theorem can take a variety of forms, such as detecting spam emails to detecting illness in the medical field.

It can as well become a bit disruptive and even I have trouble sometimes grasping the probabilities of certain situations when using Bayes' Theorem. And then I've decided to write about it and hopefully, I can help translate an important topic for others to larn from.

Let's starting time with conditional probability starting time.

Conditional probability deals with two dependent events, A and B, where event A has some effect on upshot B. In other words, the probability of event B occurring depends on Event A.

In a simple equation, conditional probability says the probability of an event A occurring, given that B occurred, 𝑃(𝐴∣𝐵), is equal to the probability that both events occur, 𝑃(𝐴∩𝐵), divided past the probability of the event B occurring lonely, 𝑃(𝐵).

Bayes' Theorem takes conditional probability a chip further. Bayes substantially substitutes variables and states the probability that both events are true, P(A∩B), is equal to a conditional probability multiplied by the probability itself.

That's a little confusing. It's easier if nosotros visualize information technology.

Conditional probability equation:

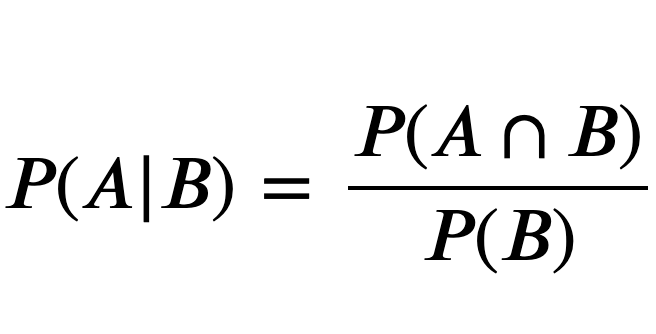
• 𝑃(𝐴∣𝐵) is the probability of event A occurring, given B has occurred. "Given" is denoted by the vertical line,|.
• 𝑃(𝐴∩𝐵) is the probability of event A occurring and event B occurring, otherwise referred to as the intersection of events A and B. The intersection is denoted by the ∩ symbol.
• 𝑃(𝐵) is the probability of just consequence B occurring.

We can utilise normal commutation to motility these probabilities around the equation. If we multiply both sides by P(B), we find that:

• 𝑃(𝐴∩𝐵) = 𝑃(𝐴∣𝐵)*𝑃(𝐵)

When 𝑃(𝐴∩𝐵) is difficult to figure out because we don't know 𝑃(𝐴∣𝐵), we tin utilize the production dominion, which derives the equation, swapping the events:

• 𝑃(𝐴∣𝐵)*𝑃(𝐵) = 𝑃(𝐵∣𝐴)*𝑃(𝐴)

Therefore,

• 𝑃(𝐴∩𝐵) = 𝑃(𝐵∣𝐴)*𝑃(𝐴)

We at present input this into the conditional probability equation, which is Bayes' Theorem:

Coolest, nerdiest sign ever? Credit: Matt Buck

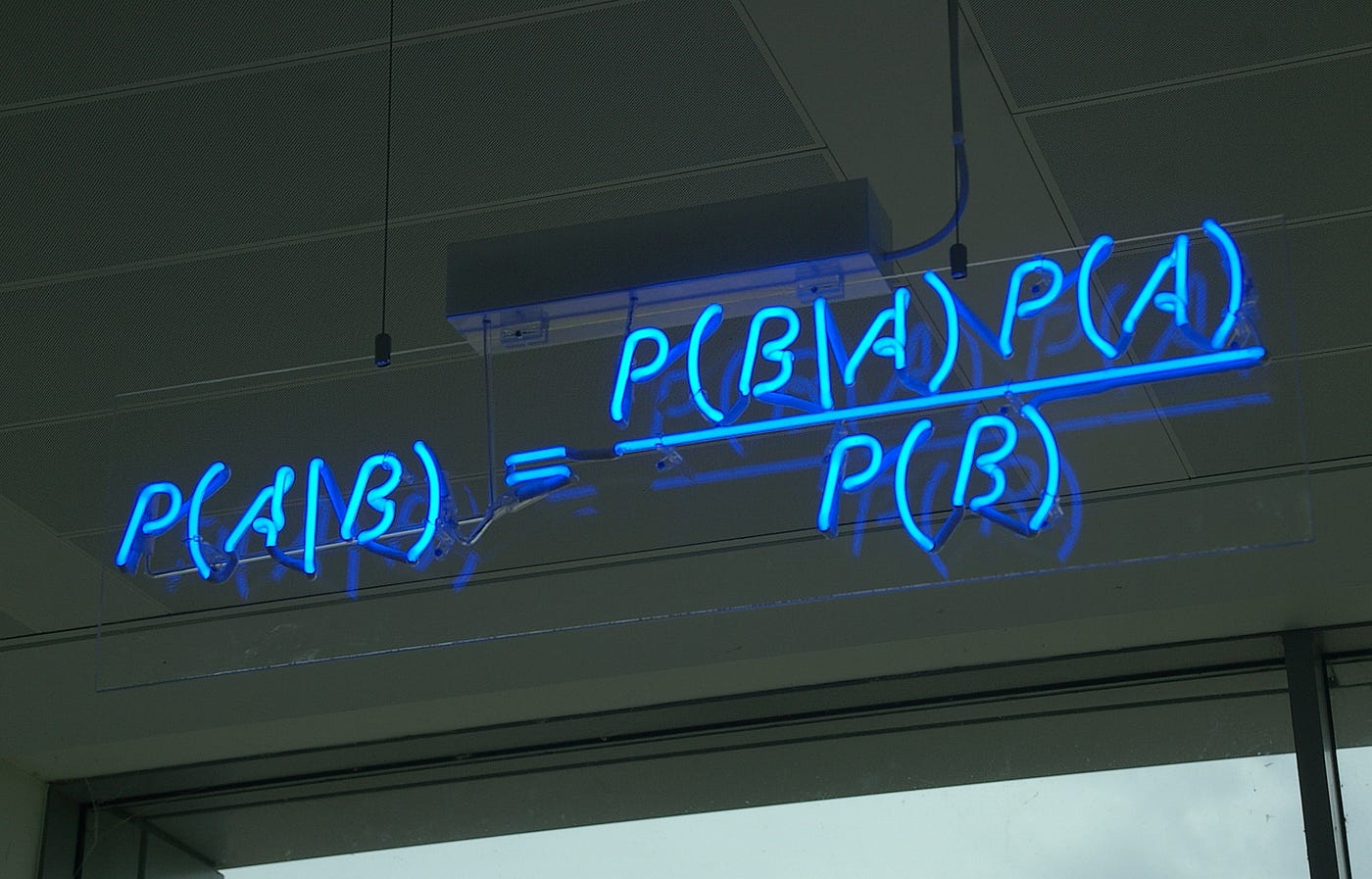
Using Bayes' Theorem, nosotros can work our way through provisional probabilities when we don't explicitly know the probability of the events intersecting, 𝑃(𝐴∩𝐵).

Bayes' Theorem can take on more complicated events as well, through partitioning, using the law of full probability. The police of full probability substantially looks at the bigger picture, enabling united states to estimate the probability of an result, past knowing the probability of the inverse: the consequence not happening. For case, the probability of event A not happening is denoted with a mark next to the event, such equally 𝑃(𝐴').

Visuals e'er brand things easier for me:

Credit: EARTHACOTTON18

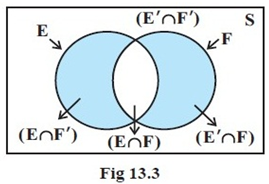
Looking at the space of effect Eastward above, using partitioning, we tin equate that the entirety of event space E is composed of (E∩F) and (East∩F′). Using this logic along with provisional probability, we can equate the post-obit:

𝑃(𝐴)=𝑃(𝐴∩𝐵)+𝑃(𝐴∩𝐵′)

𝑃(𝐴)=𝑃(𝐴∣𝐵)*𝑃(𝐵)+𝑃(𝐴∣𝐵')*𝑃(𝐵')

I want to work through a question based on Bayes' Theorem probability that you lot might encounter in a typical information science interview because they are very common and this is will also aid relate what I'g saying. Let's accept a look at a situation and interruption downwards the events into the conditional probability equation using Bayes' Theorem.

I'one thousand going to use a hypothetical conditional probability question based on contempo events. This 1 is tricky and even so gets me:

A leading coronavirus test is xc% accurate in detecting COVID. Significant if a person has COVID, they volition examination positive 90% of the time. Too pregnant if they don't have COVID, they volition test negative 90% of the fourth dimension. The estimated percentage of the population currently with COVID is v%. If a person tests positive for COVID, what's the probability that they really have COVID?

First, let'south ascertain what we know from the question:

The probability of testing positive given a person has actual COVID is 90%.

• P(positive exam|actual covid) = 0.xc

The probability of testing positive, given a person doesn't have COVID is the changed. We will denote this inverse every bit so:

• P(positive examination|actual covid') = one-P(positive exam|actual covid) = 0.ten

The per centum of the population currently with covid is 5%. In other words, the probability of having actual covid is 5%, or 0.05.

• P(actual covid) = 0.05

The probability of not having actual covid, once again, is only the inverse:

• P(actual covid') = 1-P(actual covid) = 0.95

*And finally the principal question: If a person tests positive for COVID, what's the probability that they actually take the COVID? In other words, what is the probability they have actual covid, given a positive exam?

• P(bodily covid|positive test) = ???

I know what you're thinking. "Well, the damn examination is 90% authentic, then if I test positive, it'due south a ninety% run a risk I accept bodily COVID. Correct??"

That'south what we all thought, simply Bayes' Theorem says it's more like a 32% chance.

"…What?"

I know. Literally insane. But let'due south try information technology for ourselves. Using Bayes' Theorem, form our equation for P(actual covid|positive test).

• P(actual covid|positive exam) = (P(positive exam|actual covid)*P(actual covid))/ P(positive test)

Plugging in the numbers:

• P(bodily covid|positive test) = (0.xc * 0.05)/P(positive test).

Expect- so nosotros are realizing we don't actually know the probability of but getting a positive test, with or without knowing if you have bodily COVID, P(positive test). This is where the police force of full probability comes into play! Remember: 𝑃(𝐴)=𝑃(𝐴∣𝐵)*𝑃(𝐵)+𝑃(𝐴∣𝐵')*𝑃(𝐵')

• P(positive test) = (P(positive test|bodily covid)*P(bodily covid)) + (P(positive test|actual covid')*P(actual covid'))

Now we know all of these variables.

• P(positive test) = (0.xc*0.05) + (0.x*0.95) = 0.14

Good, so we've got P(positive test), let'southward plug this back into our original Bayes' equation.

• P(bodily covid|positive examination) = (0.ninety * 0.05)/0.fourteen = 0.32

Yep, you read that correctly. Given the test is accurate a fix amount of the time, the probability of actually having COVID within that accuracy is 32%. This tin can be mind-boggling, just look at what we are working with here. Only 5% of the population has COVID. The fact that the 90% accuracy is within the pocket-sized, v% subset of the population is making a large impact.

If we were aware of additional events or information, perhaps, such equally the percentage of people testing with symptoms, this would change. Keep in heed, this is what Bayes' logic was. We can merely ameliorate our assumptions when presented with new information.

This is a part of why Bayes' Theorem and conditional probability are used so often in data scientific discipline. What we think is not always the case at all, especially when it comes to probability.

I hope you were able to at to the lowest degree somewhat understand the workings behind Bayes' Theorem, an integral part of data scientific discipline analytics. If you lot have any questions or suggestions at all, experience free to comment! I'm ever looking to learn more.

harrisdrowed.blogspot.com

Source: https://medium.com/swlh/bayes-theorem-probability-818deb5d1613

Share this post